Neural Networks for Beginners Pt.1

The world of software development is seeing some fundamental shifts with the resurgence of various AI techniques. The most significant impact has come in the form of Machine Learning and more specifically, a sub set of ML called Deep Learning. ML is simply a form of AI that enables a system to “learn” or be “trained” from data rather than through explicit programming. It is important to note that these techniques are not new. The term AI was first coined by John McCarthy back in 1956 and is defined as the capability of a machine to imitate intelligent human behavior. This shouldn’t be confused with a machine having actual intelligence or being able to generically mimic an actual human being. AI systems are designed to imitate specific human like capabilities. For example: understand language, solve specific problems, recognize sounds/images and categorize them, make predictions, etc. Each of these are very powerful capabilities, but do not reflect “actual” intelligence.

There are several different types of AI that have been researched over the years and most have gone by the wayside with machine learning have found its renaissance. Back in the 90’s, the two sub categories of AI that were most researched were ML and Expert Systems. Expert Systems are a technique whereby a system is programmed with a set of rules rather than being explicitly coded. The rules were processed by a “rules/inference engine” and could scale to handle tens of thousands of events per second even on modest hardware. The problem was that the actual rules still had to be defined by subject matter experts and were limited by the SME’s ability to figure out all the potential situations that were possible. In truth, this really isn’t AI but an approximation of it.

Machine Learning on the other hand is a technique where the software (model) learns from data rather than being created/coded or defined by software developers. The specific ML technique I’m describing in this document is known as Deep Learning or Neural Networks. I want to point out that this technique is NOT new and was originally developed back in the 60s, 70’s and 80’s. In fact, the breakthrough that made neural networks usable was called back propagation and discovered/published in 1986. Unfortunately, although the fundamental techniques to implement neural networks were well understood, they weren’t actually useful back then due to the enormous processing resources and data set sizes required to train the networks. The only commercial solution I can think of was a product from Computer Associates back in the 90’s called Neugents (part of their systems management suite). Neural Networks were abandoned by the commercial sector and most of academia with only a few Universities continuing to do research in this field; primarily here in Canada.

Back to Neural Networks which really are not very complicated at all.

Starting from the basics, a Neural Network is a collection of neurons joined together in cascading layers. The network begins with an input layer, passing through hidden layers with the results finally passing through the output layer. Before I dive into details of this structure, we need to begin with what is meant by a neuron (we don’t mean an actual living cell).

A neuron is a computation element that takes multiple inputs and computes a single output. Here’s a simple example:

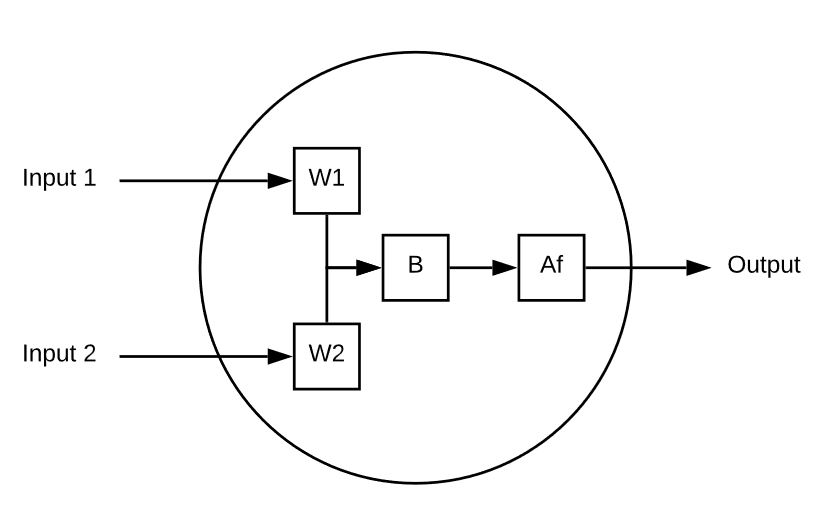
This neuron has 2 inputs.

Each Input is multiplied by weight.

The weighted inputs are then summed, and a bias value is added to that.

Finally, the unbounded value is passed through and activation function (sigmoid for example) to reduce it to a predictable range (e.g. 0 to 1).

Here’s an example of a single neuron in action:

Input 1 = 5, Input 2 = 8, W1 = 1 and W2 = .5, finally our Bias is 3

Our output looks like the following

Af( ( 5 * 1 ) + ( 8 * .5 ) + 3 )

Af( 12 ) = 0.999

Let’s try again with a different set of inputs, weights and bias:

Input 1 =-10, Input 2 = 10, W1 = 0.2, W2 = 0.1, Bias = 0.5

Output = Af( (-10 + 0.2) + ( 2 X 0.1) + 0.5)

Output = Af( -8.1 ) = 3.034

A single neuron by itself is essentially useless other than as an interesting math exercise but if we put multiple neurons together in layers we can have a neural network in the form of:

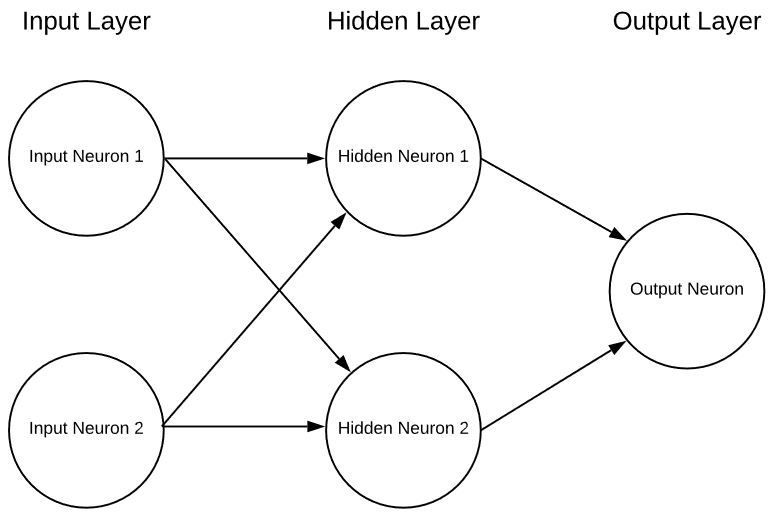
This is an extremely simplistic neural net with 2 inputs, a single hidden layer of neurons and finally a single output neuron. Neural nets can have any number of inputs, layers and any number of neurons in those layers. This flexibility is the one serious gotcha with neural networks. How does the designer of the network know what the optimal number of layers and neurons within those layers? There are some guidelines of where to start but the reality is that figuring this out is all but trial and error. Currently there is a lot of very promising research going on to help in this regard but we’re just beginning to figure this part out.

So how do you pick the right weights and biases for each neuron and how does it “learn”?

Great topic for the next installment.